refastudios.blogg.se - Finding solutions for 3 equation systems with 2 variables

FINDING SOLUTIONS FOR 3 EQUATION SYSTEMS WITH 2 VARIABLES PLUS

When an equation comprises a variable such as xx, this variable is considered to be an unknown value. Nevertheless, this lesson emphasizes exclusively equations in one variable. For illustration, x+y+7=13x+y+7=13 is an equation in double variables. It is likely for equations to have more than one variable.

FINDING SOLUTIONS FOR 3 EQUATION SYSTEMS WITH 2 VARIABLES PLUS

For instance, the equation x+3=5x+3=5, read “xx plus three equals five”, affirms that the expression x+3x+3 is equal to the value 5. These are still written by enlisting each expression on either side of an equals sign (=). In numerous cases, an equation comprises one or more variables. For instance, the assertion that “two plus five is equal to seven” is denoted by the equation 2+5=72+5=7.

Equation: A mathematical statement that proclaims the equivalence of two expressions.Īn equation is a mathematical account that states the equivalence of two expressions.

Unknown: A variable in an equation that necessitates being solved for.

Solution: A value that can be replaced for a variable to make an equation correct.

A solution of an equation can be substantiated, or checked, by replacing its value for the variable in the equation.

The values of the variables that make the equation accurate are the solutions of the equation and can be found by deciphering the equation.

When an equation comprises a variable, such as xx, the variable is measured with an unknown value.

An equation is a mathematical proclamation that proclaims the equivalence of two expressions.

(a – b) 3 = a 3 – 3a 2b + 3ab 2 – b 3 So What is an Equation?Īn equation is an expression with one variable, this variable has an answer, or value, that makes the equation accurate.įurthermore, we explain what an equation in one variable signifies and the reasons for using one.

The universal formulas used in algebra to solve algebraic equations and discover the values of unknown variables are as follows: The common arithmetic operations done in the case of algebra are as follows:

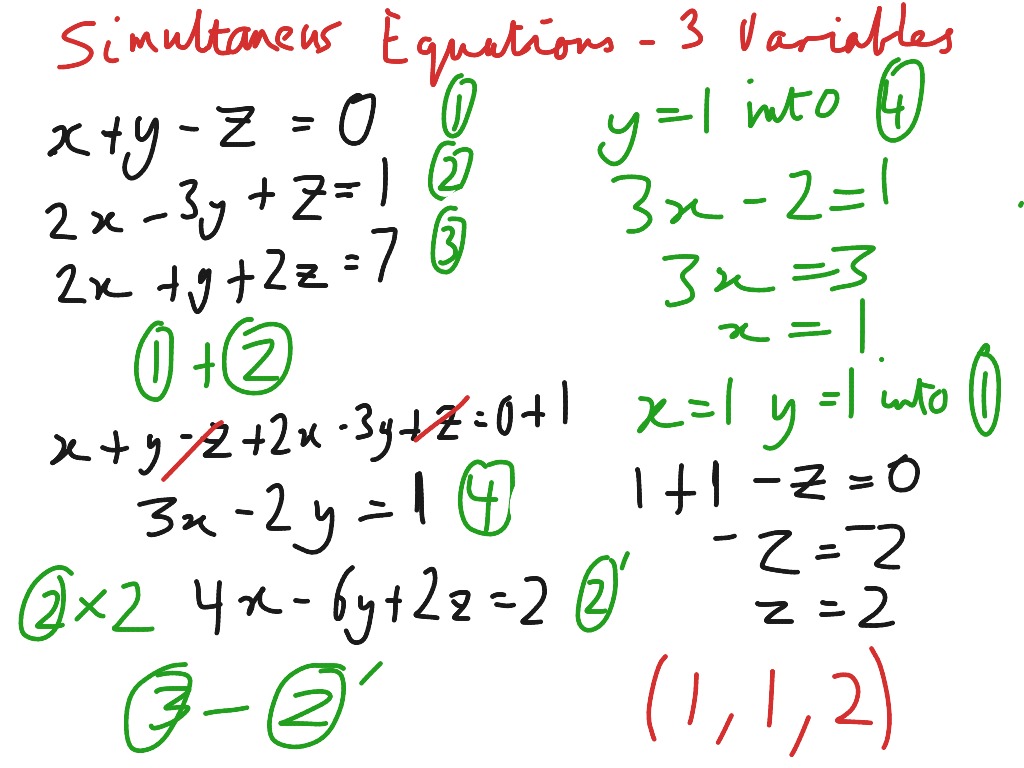
Some of the basic algebra rules are cited below: Like terms are those terms whose variables and their exponents are identical. While an expression is a group of different terms disconnected by the ‘+’ or ‘-‘ sign. Polynomial (Monomial, binomial and trinomial)Īn equation is a statement that indicates two same identities divided by the “=” sign. Some of the terms associated with basic algebra skills are cited below.ģ. When we state its fundamentals, it covers the broad algebraic expressions, formulas, and identities, which are used to solve many mathematical problems. The values which are identified in the given expression such as numbers are called constants. These alphabets are also called variables. An analogy can be made between the algebraic equation and that of a weighing scale where the weights are balanced with the help of numbers or constants.Īlgebra is the division of Maths that uses alphabetical letters to find unidentified numbers. This introduces a significant algebraic theory known as equations. By definition, it covers the simple processes of mathematics similar to addition, subtraction, multiplication, & division concerning both constant as well as variables. Before we get to learn about variable equations let us clear our concepts about the Basics of Algebra first.